atcoderで3次元累積和の問題が出て,一般化できないか考えました. 役には立たないと思います.
とりあえずatcoderの問題(3次元累積和)をおいておきます.
まずは通常の累積和(1次元累積和)を考えます.
正整数 N, 1≤x≤N を満たす整数 x に対して 整数 Ax が与えられます. Q 個のクエリが与えられるので,それぞれに答えてください.
q 個目(1≤q≤Q)のクエリでは整数 l, r (1≤l≤r≤N) が与えられるので,以下の値を求めてください.
S=x=l∑rAx- 1≤N≤2×105
- 1≤Q≤2×105
- 1≤Ax≤109
- 1≤l≤r≤N
各クエリに対して ∑x=lrAx を求めることが思い浮かびますが,これではクエリごとに計算量 O(N)となり,全体で O(NQ) なので間に合いません.
ここで以下の数列を定義します.
Si=k=1∑iAk仮にこの数列が求まっているとすれば,クエリ l,rに対して
x=l∑rAx=x=1∑rAi−x=1∑l−1Ax=Sr−Sl−1なので,O(1)で S を求めることができます.
また,Siは漸化式 Si=Si−1+Ai によって O(N)で求めることができるので,これを前計算しておけば,全体で O(N+Q) でこの問題を解くことができます.
次に2次元累積和を考えます.
正整数 N, 1≤x,y≤N を満たす整数 x と y に対して 整数 Ax,y が与えられます.
Q 個のクエリが与えられるので,それぞれに答えてください.
q 個目(1≤q≤Q)のクエリでは整数 lx,rx,ly,ry (1≤lx≤rx≤N, 1≤ly≤ry≤N) が与えられるので,以下の値を求めてください.
S=x=lx∑rxy=ly∑ryAx,y- 1≤N≤3000
- 1≤Q≤3000
- 1≤Ax,y≤109
- 1≤lx≤rx≤N
- 1≤ly≤ry≤N
この問題に対しても1次元累積和と同じように,以下の数列を定義します.
Si,j=x=1∑iy=1∑jAx,yこの数列が求まっているとすれば,クエリ lx,rx,ly,ryに対して
x=lx∑rxy=ly∑ryAx,y=Srx,ry−Slx−1,ry−Srx,ly−1+Slx−1,ly−1を計算すれば良いです.
また,Si,jは漸化式 Si,j=Si−1,j+Si,j−1−Si−1,j−1+Ai,j によって O(N2)で求めることができるので,これを前計算しておけば,全体で O(N2+Q) でこの問題を解くことができます.
この辺が怪しい人は以下の記事を読んでみてください.
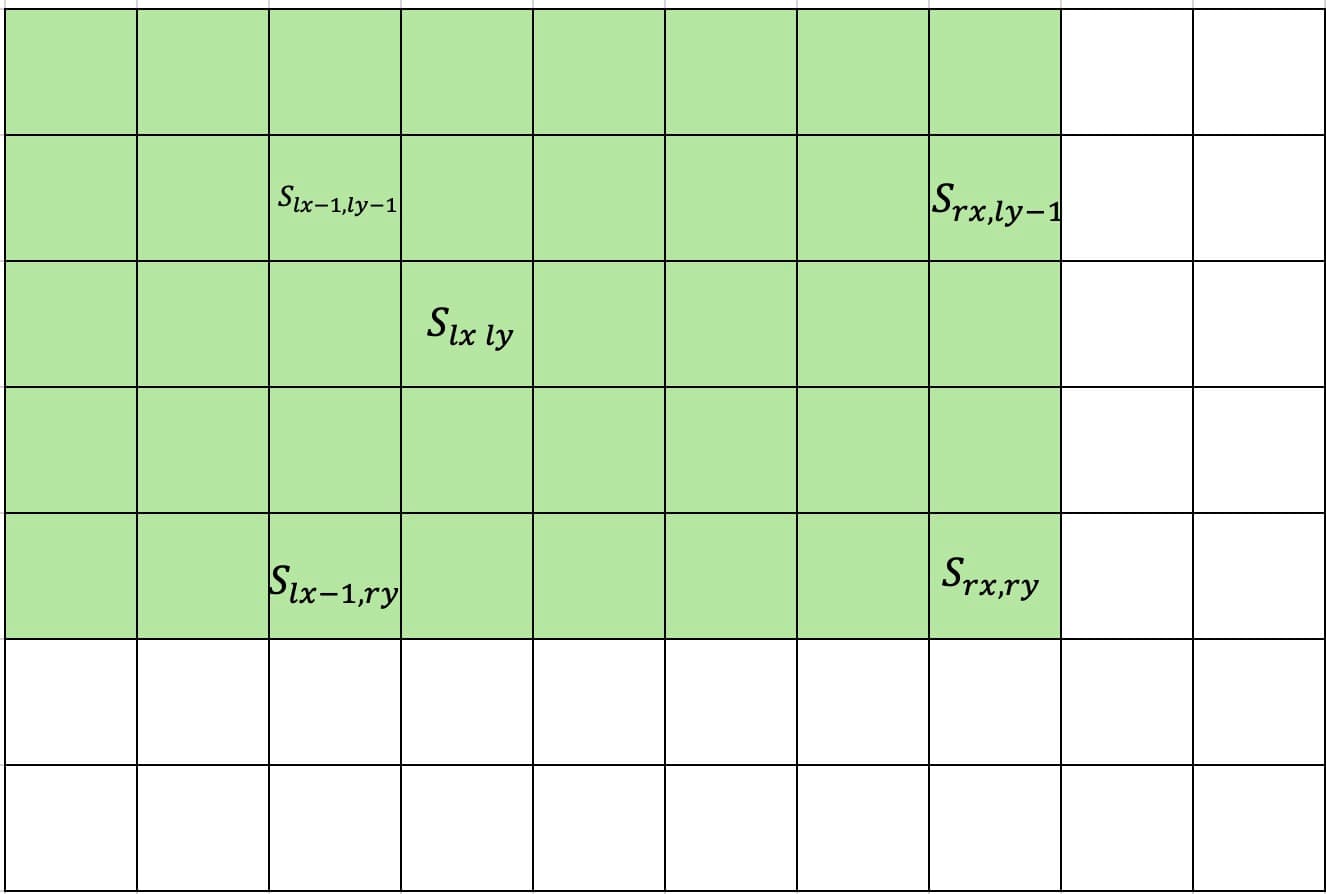
ここで, ∑x=lxrx∑y=lyryAx,y を計算する際に Slx−1,ly−1 を足しているのは,Slx−1,ly−1 が Slx−1,ry と Srx,ly−1 で重複している部分を差し引くためです.
まず範囲全体を足す.
Slx,ry−1 を引く.

同様に
Srx−1,ly を引く. ここで,
Slx−1,ly−1 を2回引いていることになる.

引きすぎてしまった
Slx−1,ly−1 を足す.

Slx,ry−1の領域を S1,Srx−1,lyの領域を S2,Slx−1,ly−1の領域を S3 とすると,
S3=S1∩S2となっていることがわかります.
また,2次元の和を求める際の式を少し変形すると,包除原理が使えそうなことがわかります.
x=lx∑rxy=ly∑ryAx,y=Srx,ry−Slx−1,ry−Srx,ly−1+Slx−1,ly−1=Srx,ry−(Slx−1,ry+Srx,ly−1−Slx−1,ly−1)=Srx,ry−(S1+S2−S3)=Srx,ry−∣S1∪S2∣数学的に正しい記述方法がわかりませんが,気持ちは伝わると思います.
これは一般に D次元累積和に拡張できます. 例えば3次元の和を求めるには,
x=lx∑rxy=ly∑ryz=lz∑rzAx,y,z=Srx,ry,rz−∣S1∪S2∪S3∣とすればよいです. ここで,S1,S2,S3 はそれぞれ Slx−1,ry,rz,Srx,ly−1,rz,Srx,ry,lz−1 の領域を表しています.
しかし,具体的な ∣S1∪S2∪S3∣ の表示が得られておらず,このままでは計算することができません.
そこで3変数の包除原理を考えます.S1∪S2=Tとおきます.
∣S1∪S2∪S3∣=∣T∪S3∣2変数の包除原理を用いて,
∣T∪S3∣=∣T∣+∣S3∣−∣T∩S3∣∣T∩S3∣について, 分配法則より
∣T∩S3∣=∣(S1∪S2)∩S3∣=∣(S1∩S3)∪(S2∩S3)∣=∣S1∩S3∣+∣S2∩S3∣−∣(S1∩S3)∩(S2∩S3)∣=∣S1∩S3∣+∣S2∩S3∣−∣S1∩S2∩S3∣となります.
また,∣T∣について,
∣T∣=∣S1∪S2∣=∣S1∣+∣S2∣−∣S1∩S2∣となり,(2),(3)を(1)に代入すると,
∣S1∪S2∪S3∣=∣S1∣+∣S2∣+∣S3∣−∣S1∩S2∣−∣S1∩S3∣−∣S2∩S3∣+∣S1∩S2∩S3∣が得られます.
ここで,
∣S1∣=Slx−1,ry,rz∣S2∣=Srx,ly−1,rz∣S3∣=Srx,ry,lz−1であり,
∣S1∩S2∣=Slx−1,ly−1,rz∣S1∩S3∣=Slx−1,ry,lz−1∣S2∩S3∣=Srx,ly−1,lz−1∣S1∩S2∩S3∣=Slx−1,ly−1,lz−1となります.
なぜならば,例えば ∣S1∩S2∣について,S1∩S2は Slx−1,ry,rz と Srx,ly−1,rz の共通した領域を表しており,z方向は rzと等しく,x,y方向はそれぞれ狭い方の領域に"縮む"ため,それぞれlx−1,ly−1となります.
それではいよいよ一般化します. まず問題を定式化します.
正整数 N, 1≤x1,x2,…,xD≤N を満たす整数 x1,x2,…,xD に対して 整数 Ax1,x2,…,xD が与えられます.
Q 個のクエリが与えられるので,それぞれに答えてください.
q 個目(1≤q≤Q)のクエリでは整数 l1,r1,l2,r2,…,lD,rD (1≤li≤ri≤N) が与えられるので,以下の値を求めてください.
S=x1=l1∑r1x2=l2∑r2…xD=lD∑rDAx1,x2,…,xD例によって累積和 Si1,i2,…,iD をO(ND)で求めておきます.
クエリ l1,r1,l2,r2,…,lD,rDに対して,
x1=l1∑r1x2=l2∑r2…xD=lD∑rDAx1,x2,…,xD=Sr1,r2,…,rD−∣S1∪S2∪…∪SD∣を計算すればよいです.
もちろんS1,S2,…,SD はそれぞれ Sl1−1,r2,…,rD,Sr1,l2−1,…,rD,…,Sr1,r2,…,lD−1 の領域を表しています.
∣S1∪S2∪…∪SD∣については,D変数の包除原理
∣S1∪S2∪…∪SD∣=i=1∑D∣Si∣−1≤i<j≤D∑∣Si∩Sj∣+1≤i<j<k≤D∑∣Si∩Sj∩Sk∣−…+(−1)D−1∣S1∩S2∩…∩SD∣によって求めることができます. 証明については省略しますが,数学的帰納法を用いることで示すことができます.
急ですがここで,Sの添字をビット表現にすることを考えます.具体的には,整数i(1≤i≤D)に対して,Sのi次元目の添字はli,riのどちらかですが,これがriのときiビット目を立てることにします.
例えば,S10110と表記したら,Sr1,l2−1,r3,r4,l5−1を表すこととします.
このように表現することで,ビットごとのAND演算を用いて集合の共通部分を簡単に求められるようになります.
例えば,∣S1∩S3∩S4∣を求めてみましょう.
S1=Sl1−1,r2,r3,r4,r5=S01111S3=Sr1,r2,l3−1,r4,r5=S11011S4=Sr1,r2,r3,l4−1,r5=S11101なので,
S1∩S3∩S4=S01111&S11011&S11101=S01001=Sl1−1,r2,l3−1,l4−1,r5とわかります.
ちなみに,包除原理を適用した際の符号に関してもビットのpop countの偶奇を見ればわかります. これは,(5)において奇数個の共通部分は+,偶数個の共通部分は−であることから従います.
このように定式化したことで,例えば3次元累積和は以下のようなコードで実装できます.
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int N, Q;
int A[110][110][110], S[110][110][110];
int L[3], R[3];
int solve() {
int sum = 0;
for(int b=0; b<1<<3; b++) {
int ind[3];
for (int i=0; i<3; i++) {
ind[i] = ((b & (1 << i)) ? L[i] - 1 : R[i]);
}
sum += S[ind[0]][ind[1]][ind[2]] * (__builtin_parity(b) ? -1 : 1);
}
return sum;
}
int main() {
cin.tie(nullptr);
ios::sync_with_stdio(false);
cin>>N;
for(int i=0; i<N; i++)for(int j=0; j<N; j++)for(int k=0; k<N; k++) cin>>A[i][j][k];
for(int i=1; i<=N; i++)for(int j=1; j<=N; j++)for(int k=1; k<=N; k++) {
L[0] = i; L[1] = j; L[2] = k;
R[0] = i; R[1] = j; R[2] = k;
S[i][j][k] = A[i-1][j-1][k-1] - solve();
}
cin>>Q;
while(Q--) {
for(int i=0; i<3; i++) cin>>L[i]>>R[i];
cout<<solve()<<endl;
}
}
これでD次元の累積和を解くことができます! 計算量はO(ND+2DQ)です.
おまけ
D=4についてやってみましょう. 未来のABCで出題されるかもしれません.
x1=l1∑r1x2=l2∑r2x3=l3∑r3x4=l4∑r4Ax1,x2,x3,x4=Sr1,r2,r3,r4−∣S1∪S2∪S3∪S4∣=Sr1,r2,r3,r4−∣S1∣−∣S2∣−∣S3∣−∣S4∣+∣S1∩S2∣+∣S1∩S3∣+∣S1∩S4∣+∣S2∩S3∣+∣S2∩S4∣+∣S3∩S4∣−∣S1∩S2∩S3∣−∣S1∩S2∩S4∣−∣S1∩S3∩S4∣−∣S2∩S3∩S4∣+∣S1∩S2∩S3∩S4∣=Sr1,r2,r3,r4−Sl1−1,r2,r3,r4−Sr1,l2−1,r3,r4−Sr1,r2,l3−1,r4−Sr1,r2,r3,l4−1+Sl1−1,l2−1,r3,r4+Sl1−1,r2,l3−1,r4+Sl1−1,r2,r3,l4−1+Sr1,l2−1,l3−1,r4+Sr1,l2−1,r3,l4−1+Sr1,r2,l3−1,l4−1−Sl1−1,l2−1,l3−1,r4−Sl1−1,l2−1,r3,l4−1−Sl1−1,r2,l3−1,l4−1−Sr1,l2−1,l3−1,l4−1+Sl1−1,l2−1,l3−1,l4−1


